Verfügbare Software für Microsoft Windows 7 / 10 / 11 ( Stand 22.07.2024 )
Die angebotene Software diente zur Unterstützung des Studiums in den unteren Semestern der Bachelor-Studiengänge der Fakultät für Elektrotechnik und Informationstechnik an der Hochschule München für angewandte Wissenschaften.
Bis zum 03.07.2024 wurden 206.025 Downloads aus den folgenden Ländern registriert: A, AL, BR, CDN, CHN, CH, CY, D, E, F, FIN, GB, I, IND, IRL, J, MD, NL, P, PL, RI, RUS, RO, S, SGP, T, TR, UA, USA, Libanon, Südkorea, Palestina, Taiwan
Die für einen sinnvollen Betrieb erforderlichen Display-Auflösungen sind in der Tabelle eingetragen.
- -->
|
ZIP- oder PDF-Datei |
Stand |
ca.-Grösse in kB |
Display (x_pix*y_pix) |
Enthaltene Datei(en) |
Nützlich für die Vorlesung(en) |
|
| 06.09.15 |
1000 |
1280 x 1024 |
ABTASTUNG |
Signale und Systeme |
||
| 06.09.15 |
1000 |
1280 x 1024 |
AD_WANDLUNG |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
ANSCHNITT |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
BILINEAR |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
BODE |
Regelungstechnik 1, Signale und Systeme |
||
|
06.09.15 |
1200 |
1280 x 1024 |
BODE_LERNEN |
Regelungstechnik 1, Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
DFT |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
DGL |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
DSP |
Signale und Systeme |
||
|
17.04.19 |
1200 |
1350 x 768 |
DREHSTROM |
Wechselstromnetze |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FALTUNG_1 |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FALTUNG_2 |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FENSTER |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FOURIER |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FOURIER_INTEGRAL |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FIR |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FOURIER_KOEFF |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FOURIER_REIHE |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
F_INT_DIMP |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
F_INT_KOEFF |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
FT_DFT_FFT |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
IIR |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
IMPULSE |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
KENNLINIE |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
POLYNOM_KENNLINIE |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
KREISDIAGRAMM |
Wechselstromnetze |
||
|
06.09.15 |
1300 |
1280 x 1024 |
LAPLACE |
Signale und Systeme |
||
|
06.09.15 |
500 |
--- |
Beschreibung zu LAPLACE |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
LEISTUNGEN |
Signale und Systeme |
||
|
|
|
1920 x 1080 |
Das Programm LINRK wird z.Zt. überarbeitet |
Regelungstechnik 1 |
||
|
|
|
--- |
Neue Beschreibung zu LINRK folgt nach Überarbeitung |
Regelungstechnik 1 |
||
|
01.04.19 |
1000 |
1920 x 1080 |
MASON, 4 Datensätze |
Regelungstechnik |
||
|
|
650 |
--- |
Beschreibung zu MASON |
Regelungstechnik |
|
|
|
06.09.15 |
1000 |
1280 x 1024 |
MISCHSPG |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
PT2 |
Regelungstechnik 1 |
||
|
06.09.15 |
1000 |
1280 x 1024 |
RINHOMOG |
Gleichstromnetze |
||
|
06.09.15 |
1000 |
1280 x 1024 |
SIGNALE |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
SI_ENTZERR |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
SPEKTRUM |
Signale und Systeme |
||
|
06.09.15 |
1000 |
1280 x 1024 |
ZEITDISK |
Signale und Systeme |
Kurzbeschreibungen der Programme
ABTASTUNG:

Das Programm veranschaulicht, wie durch Abtastung aus einem zeitkontinuierlichen ein zeitdiskretes Signal entsteht.
In einem Bild werden die Signale im Zeit- und Frequenzbereich dargestellt.
Als periodisches, zeitkontinuierliche Signal kann
1. ein Signal bestehend aus einer Frequenz oder
2. ein aus 10 Frequenzen zusammengesetztes Signal [ 'Frequenzband' ]
gewählt werden, wobei in beiden Fällen die [ maximale ] Signalfrequenz variabel ist.
Der/die Phasenwinkel können zufällig verändert werden.
Zur Signalrückgewinnung wird ein ideales Tiefpassfilter mit variabler Sperrgrenzfrequenz verwendet.
AD_WANDLUNG:
Das Programm zeigt am Beispiel einer Spannung U ( t ) = Uo + Us· sin ( 2 · pi · f · t + phi ) mit variablen Parametern alle Signalvarianten, die bei einer Abtastung mit f_abt = 10 kHz, einer wählbaren Auflösung des A / D-Wandlers ( 2 Bit bis 24 Bit ) und einer wählbaren Maximalspannung des Wandlers auftreten:
o Das "analoge" Eingangssignal U ( t ) : Wertkontinuierlich, zeitkontinuierlich
o Das abgetastete Eingangssignal U1 [ n·T_abt ] : Wertkontinuierlich, zeitdiskret
o Das quantisierte Eingangssignal U2 ( t ) : Wertdiskret, zeitkontinuierlich
o Das "digitale" abgetastete und quantisierte Signal U3 [ n·T_abt ] : Wertdiskret, zeitdiskret
o Das treppenförmige Fehlersignal Uq ( t ), das als Folge der Quantisierung entsteht: Wertkontinuierlich, zeitkontinuierlich
o Den Verlauf des Signal-Fehlers U4 ( t ) = U ( t ) - U2 ( t ) : Wertkontinuierlich, zeitkontinuierlich
Für den Wandler kann ein unipolarer oder ein bipolarer Betrieb gewählt werden, wobei im Falle einer Übersteuerung des Wandlers dies angezeigt wird.
Der Benutzer kann eines oder auch gleichzeitig mehrere dieser Signale darstellen und jeweils auch die Raster für die Abtastung wie für die Quantisierung am Display einblenden lassen.
ANSCHNITT:

Für eine unipolare oder bipolare sinusförmige Zeitfunktion mit Phasenanschnitt (Winkel variabel) können verschiedene Spektraldarstellungen ( reelle Darstellung als cosinus- / sinus- Funktionen sowie in der Form mit Betrag / Winkel gegen sinus; komplexe Darstellung nach Real- und Imaginäteil sowie nach Betrag und Winkel ) und Partialsummen mit veränderlicher Obergrenze für den Summationsindex sowie auch die Einzelschwingungen der Fourier-Reihe angezeigt werden.
Weiterhin ist auch die Darstellung des geraden und des ungeraden Anteils der Zeitfunktion möglich.
BILINEAR:

Das Programm führt in die Aufgaben und Besonderheiten der Bilinear- (oder Tustin-) Transformation ein.
1. Erklärung der Aufgabe und Herleitung der Transformations-Gleichung.
2. Vorgehen zur Umrechnung der Frequenzen beim Übergang zu zeitdiskreten Systemen.
3. Betrachtung der Bilinear-Transformation als konforme Abbildung.
4. Entwurf eines zeitdiskreten Tiefpassfilters mit wählbarer Abtastfrequenz als Beispiel.
5. Eingabe und Umrechnung von Übertragungs-Funktionen G(s) --> G(z), G(s) --> G(1/z) in der Summenform bis zum Maximalgrad n=6.
BODE:

In der vorliegenden Version bietet das Programm die folgenden Möglichkeiten:
1. Das Drucken eines Blanko-Formulars für das Bode-Diagramm im Hoch- oder Querformat,bei dem der Benutzer die Darstellungsbereiche für Omega oder die Frequenz, den Betrag und den Winkel sowie die Höhe der Diagrammteile [ in mm ] eingeben kann.
2. Das Drucken eines Bode-Diagramms (Festlegung wie unter 1. beschrieben), in dem für Betrag- und Winkelverlauf je ein Polygonzug (mit bis zu 15 Punkten) bei wählbarer Strichdicke eingetragen wird. Es ist auch möglich, die Knickpunkte in den Verläufen (wie im Bild sichtbar) zu markieren.
Das Diagramm-Formular oder das Bode-Diagramm mit Polygonzügen lässt sich auch zum Import in andere Programme als Bitmap in einer Datei BODEXX.BMP ( XX = 01 .. 99 ) abspeichern.
BODE_LERNEN:
Bei diesem Programm sind alle Darstellungen für eine Grafikauflösung von 1280 x 1024 pixels ausgelegt.
Das Programm ist in 8 Lektionen mit steigender Schwierigkeit gegliedert und soll den Benutzer mit der Darstellung der asymptotischen Näherungen als Polygonzüge im Bode-Diagramm vertraut machen.
Hier werden nur solche Funktionen betrachtet, deren (endliche) Pol- und Nullstellen auf der reellen Achse liegen.
Die 1. Lektion enthält neben Vereinbarungen zur Darstellung die mathematischen Grundlagen.
In einer kurzgefassten Wiederholung werden Logarithmen, dB-Werte, komplexe Zahlen und elementare komplexe Berechnungen,die Normierung und Entnormierung, gebrochen rationale Übertragungs-Funktionen, der Plan aller Pol- und Nullstellen sowie der Frequenzgang für den eingeschwungenen Zustand dargestellt. Insgesamt gibt es hierzu 30 Übungsaufgaben.
In der 2. Lektion werden die Vorzüge des Bode-Diagramms gegenüber anderen Darstellungen aufgezeigt, die üblichen Näherungen eingeführt und die auftretenden Steigungen im Betrags- und Phasenwinkeldiagramm betrachtet.
Die 3. Lektion befasst sich mit dem Eintragen und Ablesen von Punkten im Bode-Diagramm.
Zum Üben werden beliebig viele zufällige Aufgaben generiert.
In der 4. Lektion geht es um das Eintragen von Linien oder um das Ablesen von Linien mit deren Steigungen.
Auch hier bietet das Programm zum Üben beliebig viele zufällige Aufgaben von zwei verschiedenen Typen an.
Die 5. Lektion befasst sich mit den elementaren Frequenzabhängigkeiten PT1, I, D, PI, PD und Allpass 1. Ordnung.
20 Aufgaben und zufällig erzeugte, spezielle Übungen zum I- und D- Verhalten ermöglichen eine Erfolgskontrolle.
Die 6. Lektion behandelt Funktionen, die bei tiefen Frequenzen eine konstante Verstärkung aufweisen.
Hier sind 10 Aufgaben und 4 ausführliche Beispiele [ zu jeder Teilaufgabe kann die Lösung angezeigt werden ] vorgesehen.
In der 7. Lektion werden 5 Aufgaben und 3 ausführliche Beispiele zu Funktionen betrachtet, deren Betrag bei tiefen Frequenzen nicht konstant ist [ zu jeder Teilaufgabe kann die Lösung angezeigt werden ].
Die 8. Lektion bringt 3 weitere, ausführliche Beispiele [ zu jeder Teilaufgabe kann die Lösung angezeigt werden ].
Sie erlauben eine gute Selbstkontrolle, ob die wesentlichen Arbeiten im Bode-Diagramm nun fehlerfrei durchgeführt werden können.
Alle für die Übungsaufgaben benötigten Diagramm-Formulare können vom Programm direkt im Format DIN A4 ausgedruckt werden.
DFT:

Das Programm zeigt für einige Funktionen bei wählbarer Zahl der Stützstellen die durch Summen angenäherten reellen Koeffizienten der Fourier-Reihen.
Zum Vergleich werden auch die exakten Koeffizienten angezeigt und die relativen Fehler angegeben.
Die Partialsummen, deren Obergrenze variabel ist, zeigen mit der Modifikation nach Bessel die Interpolation des vorgegebenen Satzes von äquidistanten Stützstellen.
DGL:
Das Programm ermittelt und zeichnet die Lösung gewöhlicher, linearer DGL mit konstanten Koeffizienten und einer Ordnung n <= 3.
Neben dem Verlauf der Lösung y ( t ) können auch die Verläufe von y ' ( t ), y '' ( t ) sowie das Integral { y ( t ) dt } dargestellt werden.
Für die Störfunktion x ( t ) stehen zwei allgemeine Funktionen zur Wahl, deren Kennwerte vom Benutzer einzugeben sind:
x1 ( t ) = K0 + K1*t + K2*t² + K3*t³
x2 ( t ) = K0 * exp( K1 * t ) * sin ( K3 * t + K4 )
Als Anfangswerte können vorgegeben werden:
y( t=0 ), y '( t=0 ), y ''( t=0 )
Da das Programm die Laplace-Transformation zur Lösung verwendet, kann auch die Bildfunktion des aktuell betrachteten Signals (als gebrochen rationale Funktion und als deren Partialbruch-Zerlegung) angezeigt werden.
Die Zeitfunktionen der Signale lassen sich ebenfalls anzeigen.
DREHSTROM:
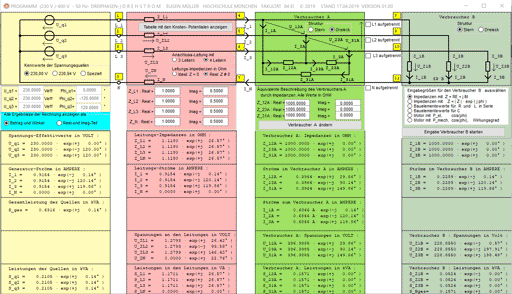
Mit dem Programm können Ströme, Spannungen und Leistungen in einem 50 Hz-Dreiphasen-Drehstromsystem berechnet werden.
Die Generator-Spannungen sind ebenso wählbar wie die Zahl der Leitungen (mit oder ohne Leitungsimpedanzen).
Zwei Verbraucher können als Stern- oder Dreieckschaltungen betrieben und deren Elementewerte in verschiedenen Formen eingegben wereden.
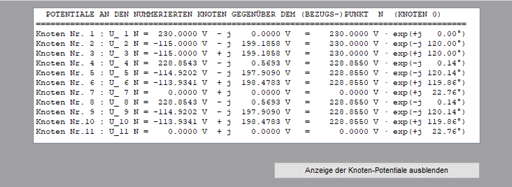
Die Potentiale an den elf Knoten der Anordnung lassen sich als Anzeige einblenden.
Alle Ergebnisse können wahlweise in kartesischer oder polarer Form dargestellt werden.
FALTUNG_1:

Das Programm dient der Veranschaulichung der Faltungs-Operation mit wählbaren Eingangssignalen und wählbaren, typischen Einheits-Impuls-Antworten von Systemen erster und zweiter Ordnung.
Bei der Betrachtung werden aus Grüden einer übersichtlichen Darstellung kontinuierliche Signale durch eine Folge von Impulsen angenähert.
Der linke Bildteil zeigt anschaulich und leicht verständlich, wie man sich die Ausführung der Faltungs-Operation vorstellen kann:
Das Ausgangssignal wird dabei auf gewichtete und verschobene Einheits-Impuls-Antworten zurückgeführt, deren Integration [ in der hier dargestellten Näherung ihre Summation ] das Ausgangssignal ergibt.
Im rechten Bildteil ist abstrakter und nicht so leicht zu verstehen auch die [durch eine Summe angenäherte] Ausführung des Faltungsintegrals durch Klappen, Verschieben und Bewerten der Einheits-Impuls-Antwort zu sehen.
Die wesentliche Erkenntnis ist dabei, dass beide Betrachtungen zum gleichen Ergebnis führen.
Zu beiden Varianten stehen dem Benutzer weitere Erklärungen zur Verfügung.
Wählbar ist auch eine Darstellung mit der Nomenklatur zeitdiskreter Vorgänge zur Auswertung der Faltungssumme.
Die Faltung kann manuell in Einzelschritten oder auch automatisch als Animation durchgeführt werden.
FALTUNG_2:

Das Programm zeigt anhand von drei Beispielen die Ausführung der Faltungs-Operation.
Der Benutzer kann wählen, welches der beiden Signale umgeklappt ("gefaltet") wird und erkennt, dass in beiden Fällen das Ergebnis identisch ist.
Die grün eingetragene bewertete "Überlappungsfläche" beider Signale entspricht zu jedem Zeitpunkt dem Wert des Ausgangssignals a(t).
Die Zeit t kann durch Verstellen der Position des Schiebereglers variiert werden.
FENSTER:

Mit dem Programm können Signale im Zeit- und im Frequenzbereich dargestellt werden, die aus zwei sinusförmigen Anteilen mit wählbaren Frequenzen bestehen.
Darüber hinaus stehen einige Fensterfunktionen [ Rechteck, Dreieck, Hann, Hamming, Blackman, Kaiser ] zur Verfügung, die mit den Signalen im Zeitbereich multipliziert werden können. Die zugehörigen Betragsspektren lassen sich linear oder in dB darstellen.
Die Signale werden nur zeitdiskret betrachtet.
FIR:

Mit dem Programm kann die zeitdiskrete Signalverarbeitung in einem FIR-Filter mit 5 Verzögerungen schrittweise und als Animation bei verschiedenen Eingangssignalen beobachtet werden.
Die Koeffizienten des Transversalfilters lassen sich auswählen oder auch manuell eingeben.

Die zugehörigen Frequenzgänge von Betrag ( linear oder in dB ) und Winkel lassen sich ebenfalls darstellen.
FOURIER:

Der Benutzer kann bei drei periodischen, symmetrischen Funktionen f(x) die Ermittlung der reellen Fourier-Koeffizienten a1 - a5 und b1 - b5 anschaulich an Hand der Verläufe sowie der Beiträge zum Integral [ die als schraffierte Teil-Flächen dargestellt sind ] verfolgen.
Diese Darstellungen zeigen, warum gewisse Koeffizienten in den Fourier-Reihen symmetrischer Zeitfunktionen entfallen.
FOURIER_INTEGRAL:

Für einmalige Zeitfunktionen können deren gerade und ungerade Anteile sowie die zugehörigen Spektraldichte-Funktionen nach Betrag und Winkel sowie nach Realteil und Imaginärteil dargestellt werden.
Der Benutzer kann selbst Zeitfunktionen als Polygonzüge mit maximal 20 Stützstellen eingeben oder vorbereitete Funktionen aus einer Liste übernehmen.
FOURIER_KOEFF:

Für periodische, polygonzugartige Zeitfunktionen können deren reelle und komplexe Fourier-Koeffizienten exakt berechnet und dargestellt werden.
Der Benutzer kann selbst Zeitfunktionen mit maximal 11 Stützstellen eingeben.
FOURIER_REIHE:

Für eine Anzahl nichtsinusförmiger periodischer Zeitfunktionen können verschiedene Spektraldarstellungen ( reelle Darstellung als cosinus- / sinus- Funktionen sowie in der Form mit Betrag / Winkel gegen sinus; komplexe Darstellung nach Real- und Imaginäteil sowie nach Betrag und Winkel ) und Partialsummen mit veränderlicher Obergrenze sowie auch die Einzelschwingungen der Fourier-Reihen angezeigt werden.
Die periodischen Funktionen lassen sich auch als akustische Signale mit einer Grundfrequenz von 300 Hz per Soundkarte und Lautsprecher ausgeben.
Das Gibbs'sche Phänomen lässt sich gut betrachten, da die Maximalzeit der Darstellung variabel ausgeführt ist.
Weiterhin ist auch die Darstellung des geraden und des ungeraden Anteils der Zeitfunktionen möglich.
F_INT_DIMP:

Drei wählbare Impulsformen (Rechteck-, Dreieck-, 1-cos²-Form) können direkt oder nach der Zeit abgeleitet als Einzel- oder als Doppelimpuls betrachtet werden.
Die zugehörige Spektraldichtefunktion lässt sich nach Betrag und Winkel sowie nach Real- und Imaginärteil darstellen.
Der Benutzer kann die Amplitude(n), Breite(n) und die zeitliche(n) Verschiebung(en) per Eingabe verändern und auch den darzustellenden Frequenzbereich festlegen.
F_INT_KOEFF:

Das Programm verdeutlicht mit einem einblendbaren Text und mit Bildern, wie sich aus der Spektraldichte-Funktion eines einmaligen Signals U(t) die komplexen Fourier-Koeffizienten C_n eines aus U(t) ermittelten, periodisch fortgesetzten Signals Up(t) [ nach einer Idee von Norbert Geng ] berechnen lassen.
Für einmalige Zeitfunktionen U(t) können deren Spektraldichte-Funktionen U(f) nach Betrag (linear oder in dB) und Winkel dargestellt werden.
Auf die gleiche Weise können auch die Linienspektren der periodisch fortgesetzten Funktionen angezeigt werden.
Der Benutzer kann selbst Zeitfunktionen mit maximal 20 Stützstellen eingeben oder vorbereitete Funktionen aus einer Liste übernehmen.
Der Benutzer kann weiterhin die Periodendauer T für die Fortsetzung der einmaligen Zeitfunktion wie auch die maximale Frequenz für die Darstellung der Spektren einstellen.
FT_DFT_FFT:

Für eine Anzahl einmaliger Zeitfunktionen können die Fourier-Transformierten der zeitkontinuierlichen und zeitdiskreten Darstellung angezeigt werden.
In allen Fällen ist der Übergang vom Fourier-Integral zur DFT / FFT ersichtlich.
Die Frequenzachse kann wahlweise fest oder variabel festgelegt werden.
Abtastfrequenz und Periodendauer lassen sich verändern.
IIR:

Mit dem Programm kann die zeitdiskrete Signalverarbeitung in einem IIR-Filter zweiter Ordnung (Direktform-II-Struktur) schrittweise und als Animation bei verschiedenen Eingangssignalen im Zeitbereich beobachtet werden.
Als Eingangssignale sind wählbar:
o Einheits-Impuls-Folge
o Einheits-Sprung-Folge
o Rampenförmige Folge
o Sinus- und Cosinus-Folgen verschiedener Frequenzen
Für die Filterkoeffizienten stehen 10 wählbare Datensätze für TP und HP verschiedener Approximationen bereit. Eine manuelle Eingabe der Koeffizienten ist ebenfalls möglich.
Alle Berechnungen können mit den exakten Koeffizienten wie auch mit quantisierten Koeffizienten [ 3 Bit - 64 Bit incl. VZ ] durchgeführt werden.
Die Auswirkungen von Überschreitungen des Zahlenbereichs [ -2 ... +2 ] im Inneren des Filters lassen sich mit drei Varianten der Überlaufbehandlung untersuchen:
o Lineare Kennlinie, unbegrenzter Zahlenbereich, keine Überlaufprobleme
o Sättigungskennlinie , Begrenzung der Zahlen auf den Bereich [ -2 ... +2 ]
o Sägezahnkennlinie wie beim Überlauf der Rechnung mit 2er-Komplement-Zahlen
Die bei einer eingestellten Wortlänge für die Koeffizienten möglichen stabilen Pollagen können in der z-Ebene dargestellt werden.
Die zugehörigen Frequenzgänge von Betrag ( linear oder in dB ) und Winkel lassen sich ebenfalls darstellen.
IMPULSE:

Der Benutzer kann wählbare, vorgegebene oder selbst eingegebene reelle Impulsfolgen im Zeitbereich mit der Zerlegung in den geraden und ungeraden Anteil wie auch die zugehörige Fourier-Transformierte im Spektralbereich (nach Real- und Imaginärteil sowie nach Betrag und Winkel) darstellen.
Die obere Frequenzgrenze für die beiden Darstellungen der Spektralfunktion ist wählbar.
Dadurch kann man z.B. die Auswirkung einer Zeitverschiebung auf die Spektralfunktion gut beobachten und leichter verstehen.
Die Impulse (Zeitbereich: -10 <= k <= 10) können mit den Werten -1, -0.75, -0.5, -0.25, 0, 0.25, 0.5, 0.75 und 1 belegt werden.
KENNLINIE:

Auf eine von 15 wählbaren statischen Kennlinen y(x) wirkt als Signal die Zeitfunktion x(t)=sin(w1*t) oder x(t) = cos(w1*t).
Am Bildschirm werden dargestellt:
Als Graphen: Die Kennlinie y(x), das "Eingangs-Signal" x(t), das "Ausgangs-Signal" y(t).
Die reellen Fourier-Koeffizienten a[n], b[n] : Zahlenwerte tabelliert und als Linienspektren.
Kennwerte von y(t) : Gleichanteil, Effektivwert und Klirrfaktor.
Für den Fall, dass man die Kennlinie einem nichtlinearen Bauteil zuschreibt, das an einer sinusförmigen Spannung betrieben wird, werden auch die umgesetzten Leistungen (Scheinleistung S, Wirkleistung P, Blindleistung Q) berechnet und angezeigt.
Der Benutzer kann sich auch die Hilfslinien zur punktweisen Konstruktion des Verlaufs von y(t) eintragen lassen.
POLYNOM_KENNLINIE:

An einem Bauelement mit der statischen Strom-Spannungs-Kennlinie
i(u) = c0 + c1*u + c2*u*u + c3*u*u*u + c4*u*u*u*u
liegt wahlweise die Spannung u(t) = U0 + U1*sin(w1*t) oder u(t) = U0 + U1*cos(w1*t).
Die Koeffizienten c0, c1, c2, c3 und c4 sowie die Werte der Spannungen U0 und U1 kann der Benutzer eingeben. Dargestellt wird neben dem Verlauf der Spannung u(t) die Kennlinie i(u). Berechnet und angezeigt werden darüberhinaus der Verlauf i(t) des Stroms und die Koeffizienten der zugehörigen reellen Fourier-Reihe sowie die in dem Bauelement umgesetzten Leistungen.
Der Benutzer kann sich auch die Hilfslinien zur punktweisen Konstruktion des Verlaufs von i(t) eintragen lassen.
KREISDIAGRAMM:
.gif)
Im Kreisdiagramm lassen sich die Transformationswege zur "Anpassung" einer komplexen Impedanz >Z_aus< an eine zweite komplexe Impedanz >Z_ein < durch ein Netzwerk mit zwei idealen Blindelementen untersuchen und darstellen.
Die beiden -aus je bis zu zwei Bauelementen bestehenden- Impedanzen können über normierte oder technische Werte als Serien- oder Parallelschaltung eingegeben werden.
Anzeigen lassen sich alle möglichen Transformationsnetzwerke sowie die zugehörigen Transformationswege. Die Auswirkung von Toleranzeinflüssen (siehe dazu das Bild oben) lassen sich ebenso anzeigen, wie die Strom- und Spannungsverhältnisse an den Klemmen / im Inneren der Netzwerke.
LAPLACE:
Programm für alle elementaren Berechnungen und Darstellungen zu gebrochen rationalen Bild- und Übertragungs-Funktionen.
Die Eingabe erfolgt im Bildbereich durch bis zu vier Teilfunktionen.
Berechnet werden u.a. PN-Plan, Zeitverhalten, Partialbruch-Zerlegung, Bode-Diagramm, ...
Das Programm bietet vielfältige Möglichkeiten zur Umrechnung von Funktionen:
EIA(t), ESA(t), PBZ, G(s)=EIA(s), ESA(s), Summenform <--> Produktform.
Die Kennwerte der Teilfunktionen lassen sich für eine Monte-Carlo-Analyse mit Toleranzen versehen.
Zu diesem Programm steht eine Anleitung / Beschreibung ( Umfang 20 Seiten ) im PDF-Format zum Download zur Verfügung.
LEISTUNGEN:

Der Benutzer kann für die periodische Spannung u(t) und für den periodischen Strom i(t) neben einem Gleichanteil bis zu drei Harmonische nach Betrag und Winkel eingeben.
Dargestellt werden die Verläfe von u(t) und i(t) sowie die zugehörigen Linienspektren.
Die Beiträge zur Wirk-, Blind-, Verzerrungs- und Scheinleistung erscheinen zahlenmäsig in Tabellenform, damit die Auswirkungen der einzelnen Frequenzen verständlich werden.
Für die unterschiedlichen Leistungen werden auch erklärende Texte angeboten.
Die Klirrfaktoren von Strom und Spannung werden berechnet und angezeigt.
LINRK:

Das schnell zu erlernende und leicht zu bedienende Simulationsprogramm erlaubt alle elementaren Berechnungen und Darstellungen, die an einem einmaschigen, linearen Regelkreis möglich sind.
Die Eingabe erfolgt blockorientiert. Optimierung von Führungs- und Störverhalten, Minimierung der Ausregelzeit, Vorgabe des maximalen Überschwingens, Identifikation anhand des Bode-Diagramms und der Einheits-Sprung-Antwort (ESA).
Die Wurzelortskurve kann für sich alleine oder zusammen mit der ESA ( siehe Bild ) bzw. mit dem Bode-Diagramm dargestellt werden.
Das Programm bietet vielfältige Möglichkeiten zur Umrechnung von Funktionen:
EIA(t), ESA(t), Partialbruch-Zerlegung, G(s)=EIA(s), ESA(s), Summenform <--> Produktform.
Die Kennwerte der Blöcke lassen sich für eine Monte-Carlo- Analyse mit Toleranzen versehen.
Die Datensätze für die Übungen zur Vorlesung Regelungstechnik 1 sind enthalten.
Zu diesem Programm steht eine Anleitung / Beschreibung ( Umfang 27 Seiten ) im PDF-Format zum Download zur Verfügung.
MASON:
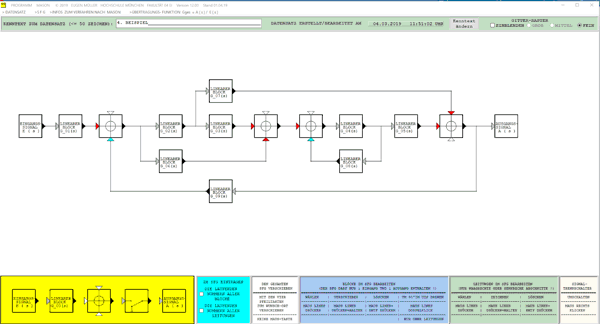
Programm zum Erlernen der Methode nach MASON zur Berechnung der resultierenden Übertragungs-Funktion vermaschter Signalflussgraphen mit bis zu fünf Rückkopplungs-Kreisen, die sich nicht berühren.
In der Datei MASON.PDF wird auf 17 Seiten das Verfahren an vier Beispielen erklärt und die Bedienung des Programms erläutert.
Allgemeine Informationen zum Verfahren sowie Zwischenergebnisse ( Anzahl der Vorwärts-Pfade, Anzahl der Rückkopplungs-Kreise usw. ) können angezeigt werden.
MISCHSPG:

Eine aus einem Gleichanteil und vier sinusförmigen Wechselspannungen (mit den Kreisfrequenzen w1, 2 w1, 3 w1, 4 w1) zusammengesetzte Mischspannung mit eingebbaren Kennwerten wirkt auf ein passives RLC- Netzwerk vom Grad n=2 (Struktur vorgegeben, Elementewerte eingebbar).
Der Benutzer kann eine von fünf Spannungen als Ausgangsgrösse Ua wählen.
Am Bildschirm werden die Zeitfunktionen am Eingang Ue(t) und Ausgang Ua(t) sowie die Frequenzgänge zu Betrag und Winkel von Ua(jw) / Ue(jw) tabellarisch und als Graphen dargestellt.
Die Effektivwerte und die Klirrfaktoren beider Signale werden ebenfalls angegeben.
PT2:

Demonstrationsprogramm für die vier gebräuchlichen Varianten eines PT2-Gliedes.
Zu jeder Variante wird ein Informationstext angezeigt.
Die folgenden Darstellungen sind vorgesehen:
Mit festen Kennwerten: PN-Plan, 3D-Bild des Betrages, Bode-Diagramm, Einheits-Impuls-Antwort, Einheits-Sprung-Antwort
Mit einem variablen Kennwert: PN-Plan, Bode-Diagramm, Einheits-Impuls-Antwort, Einheits-Sprung-Antwort.
RINHOMOG:

Mit dem Programm kann (in einer guten Näherung) neben dem wirksamen Widerstand auch die Verteilung der Äquipotentiallinien in einer ebenen Widerstands-Anordnung berechnet werden.
Dazu wird ein rechteckiger Bereich des Displays durch ein Gitterraster in Quadrate mit einer wählbaren Kantenlänge zwischen 16 Pixel (siehe oberes Bild) und 60 Pixel (siehe unteres Bild) unterteilt.
Jedem Quadrat kann der Benutzer eine der folgenden Eigenschaften zugeweisen, die am Display in verschiedenen Farben dargestellt werden:
o Sehr gut leitende positive Elektrode
o Sehr gut leitende negative Elektrode
o Widerstandsmaterial 1 (Flächenwiderstand fest R_Fläche 1 = 1 Ohm)
o Widerstandsmaterial 2 (Flächenwiderstand wählbar R_Fläche 2 = 0.1 .. 10 Ohm)
o Isolator mit sehr geringer Leitfähigkeit
Jedes Quadrat wird durch eine Ersatzschaltung bestehend aus vier gleichen Widerständen mit dem Wert R = 2* R_Fläche an den Außenkanten dargestellt.
An den Elektroden wirkt eine Quelle mit einem konstanten Gleichstrom von Io = 1 A und das Programm berechnet alle Knotenpotentiale des gesamten Widerstandsnetzwerks durch die Lösung des zugehörigen linearen Gleichungssystems mit dem Gauß-Algorithmus und Spaltenpivotisierung.
Neben dem zwischen den Elektroden wirksamen Ersatzwiderstand werden durch lineare Interplation aus den Knotenpotentialen die Verläufe einer wählbaren Anzahl von Äquipotentiallinien als Polygonzüge berechnet.
Abhängig von der Bildschirmauflösung und dem eingestellten Gitterraster kann der Umfang des Gleichungssystems sehr groß und der zur Lösung erforderliche Rechenaufwand erheblich werden.
Bei der maximal durch das Programm unterstützten Displaygröße von 1920 x 1080 Bildpunkten und dem feinsten, möglichen Gitterraster im Abstand von 16 Pixel sind 6426 Gleichungen zu lösen.
Ein erklärender Text gibt Hinweise auf Besonderheiten und erklärt an einem Anwendungsbeispiel auch den Begriff des Flächenwiderstandes R_Fläche.
SIGNALE:

Im Programm wird ein Signal untersucht, das aus 1 bis 4 sinusförmigen Schwingungen zusammengesetzt ist. Die Nullphasenwinkel der Schwingungen können mit zufällig gewählten Werten belegt werden .
Das Programm zeigt Zeitverläufe und Spektren des Signals, wobei für die Darstellung alle Kombinationen von zeitkontinuierlich / zeitdiskret sowie wertkontinuierlich / wertdiskret wählbar sind.
Die Abtastfrequenz kann ebenso verändert werden wie auch die Anzahl der bits zur Quantisierung.
Auch das auftretende 'Quantisierungs-Geräusch' ist im Zeit- und Frequenzbereich darstellbar.
SI_ENTZERR:

Das Programm berechnet optimale Betragsentzerrer zum Ausgleich der Änderungen im Betragsfrequenzgang, die durch ein Sample + Hold - Glied in zeitdiskreten Systemen hervorgerufen werden.
Dargestellt werden die Frequenzgänge der si(x)-Verzerrung, des Entzerrers sowie des Gesamtverhaltens.
Die Übertragungs-Funktion des Entzerrers G_entz(s) ist auf die Abtastfrequenz fs normiert.
Der Benutzer wählt die Ordnung ( 1 oder 2 ) des Entzerrers und die obere Grenze des Nutzfrequenzbandes f max = 0.1*fs .... 0.5*fs .
Die Optimierung stellt sicher, dass der Betragsfehler minimal wird und im Nutzband [ 0 <= f <= f max ] gleichmäßig schwankend verläuft.
Da die Minimal- und Maximalwerte für die Darstellung des Betrages vom Benutzer verändert werden können, lassen sich auch kleine Schwankungen um den Sollwert erkennen.
SPEKTRUM:

Programm zur Darstellung von periodischen Zeitfunktionen und deren Betragsspektren, die mit der FFT berechnet werden.
Der Benutzer wählt :
die Zeitfunktion und deren Dauer
die Abtastfrequenz und bei Bedarf eine Quantisierung
die Art und die Breite der Fensterfunktion
die Achsenteilung des Spektrums ( linear oder logarithmisch )
Mit SPEKTRUM lassen sich die wichtigsten Besonderheiten der FFT relativ leicht visualisieren und verstehen.
ZEITDISK:

Programm zur Auswertung und Darstellung von Differenzengleichungen, Übertragungs-Funktionen G(z) und G(1/z) kausaler Systeme.
Der Grad der Funktion muss im Bereich 1 <= n <= 6 liegen.
Der Frequenzgang, der PN-Plan sowie die zugehörigen Einheits-Impuls- und Einheits-Sprung-Antworten werden berechnet und angezeigt.
Der Betrag der Funktion kann über einem Ausschnitt der z-Ebene als Pseudo-3D-Bild dargestellt werden.
© Copyright Eugen Müller 2024

